Swami Vivekananda’s luminous mind probed virtually every domain of human excellence to its depth and came up with astounding revelations. Little known however is his mastery of the nuances of probability theory in Statistics. This article gives us a peep into this hither-tounknown aspect of Swamiji.
Prologue
English qualifiers bearing on greatness might well be vying with each other to represent the manysplendored personality of Swami Vivekananda. Be that as it may, Swami Vivekananda defies superlatives. Had he only delivered that supremely felicitous speech in Chicago on 11th September’1893, his place in the religious history of the world would have been assured. Had his only contribution to the world-thought been the unique presentation of four Yogas – Jnana, Bhakti, Raja, and Karma and their integration, he would be acclaimed as the prophet of synthesis. Had he only founded the Ramakrishna Math and the Ramakrishna Mission, he would have been immortalized as the creator of a new face of monasticism. Had his only gift to the world literary been his celebrated travelogue written in colloquial Bengali, he would be hailed today as the originator of a new style in Bengali literature. That he gave us all these and more – so much more – is our great good fortune and is a testament to the power of an extraordinary soul-force being brought to bear upon diverse domains of human endeavors. No wonder, this ‘prophet of infinitude’1 appears in a mind- boggling multiplicity of roles – religiousteacher, philosopher, historian, patriot, social & economic thinker, litterateur, humorist, singer, sportsman ……. indeed the list could go on. Can we possibly see a ‘Probabilist’ somewhere down the list? Or, is it too farfetched to be true? Well, not really. Let us read on.

Dice-Playing, Immortality, and the Sannyasi
While the great theoretical Physicist Albert Einstein – for fear of vitiating Nature’s determinism – would not have God playing dice with the universe, Swami Vivekananda – arguably the greatest champion of God – found the creator to be a consummated ice – player ! Interestingly enough, Swamiji’s ascription of dice-playing to God does not make Him (God) a capricious Being – rather, in and through God’s created universe, what shows through is a ‘specialized’ deterministic pattern, powered by the ‘law of chance’. Surely, never before or since had the secular science of Probability been placed on such a sacred footing!
The context of Swamiji’s reaching out to the theory of Probability is as exciting as it can possibly get. He was talking on ‘Immortality’ to an American audience. Decidedly the topic was such as to have all the listeners hanging on his words. Who does not want to live forever? While various theological traditions might well expatiate on the ‘implied’ meaning of ‘Immortality’ (i.e. it is the spiritual Self that is immortal), it is idle to deny that it’s the ‘ literal ’ meaning of ‘Immortality’ that holds the fascination for man. None can help wondering: can I continue living forever as the ‘person’ that I currently am? Theological traditions, having no answer to provide, at best promise a heaven after death. But, Swamiji took up the gauntlet. Using an argument which is a logical tour de force in itself, he proceeded to show how even the ‘formed’ beings, by way of continuation, can recur – albeit at certain periodic intervals. Like an accomplished ‘Probabilist’ he marshalled his facts:
‘In one sense bodies and forms even are eternal. How? Suppose we take a number of dice and throw them, and they fall in this ratio — 6 — 5 — 3 — 4. We take the dice up and throw them again and again; there must be a time when the same numbers will come again; the same combination must come. Now each particle, each atom, that is in this universe, I take for such a die, and these are being thrown out and combined again and again. All these forms before you are one combination. Here are the forms of a glass, a table, a pitcher of water, and so forth. This is one combination; in time, it will all break. But there must come a time when exactly the same combination comes again, when you will be here, and this form will be here, this subject will be talked, and this pitcher will be here. An infinite number of times this has been, and an infinite number of times this will be repeated.’2
The thoughtful reader will not fail to recognize that the whole argument above rests on the large repetitions of the dice-throwing experiment and the assurance of the recurrence of a set of outcomes that occurred at a specific throw. Now, the conclusion of the certainty of recurrence of a specific set (i.e., ‘there must be a time when the same numbers will come again’) in a series of random occurrences is something that a person with a fair degree of acquaintance with probability theory can make. We might as well try to trace Swamiji’s thought process here with regards to his example of throwing four dice simultaneously and observing an outcome {6,5,3,4}. This outcome, the Probabilist in Swamiji asserts, must occur again if the experiment of throwing the four dice is repeated very many times (‘We take the dice up and throw them again and again.’). How did he arrive at this? Here is the little calculation along with certain a-priori assumptions that might have raced through his phenomenal intellect:
While the great theoretical
Physicist Albert Einstein – for
fear of vitiating Nature’s
determinism – would not have
God playing dice with the
universe, Swami Vivekananda –
arguably the greatest champion
of God – found the creator to be
a consummate dice-player!
Assuming (a) each die is fair i.e., its six faces are equally likely to occur (b) the experiment of casting four dice simultaneously is repeated ‘n’ times (c) the outcomes of each of the four dice in any experiment are independent (d) all the ‘n’ experiments are independent, the probability that the outcome {6,5,3,4} does not occur in any of the ‘n’ experiments is (1 – 1/64 ) n i.e., (1295/1296)n . Now, the chance that the set {6,5,3,4} occurs at least once is {1 – (1295/1296)n }. As ‘n’ gets larger and larger, the probability of the set {6,5,3,4} occurring at least once tends towards 1 i.e., certainty! (In fact, with n = 10,000, this probability is approximately 0.9995).
Voila! It’s truly amazing how Swamiji made use of this nascent science of chance (at least it was so during 19th century) to make some hither-to unheard-of remarks on ‘Immortality’ of bodies and forms, hastening to point out however that ‘that is not the immortality of the soul.’3 Anyway, as the purpose of this article is to understand Swamiji as the ‘Probabilist’, we will confine our discussion to ‘Immortality’ of bodies and forms upon which Swamiji so adroitly brings to bear the ‘Law of Chance’. In yet another lecture, ‘The Atman: Its Bondage and Freedom’, Swamiji illustrates the same idea using almost the same example, with an additional idea of Probability-theory thrown in:
‘All the forms which we are seeing now have been manifested again and again, and the world in which we live has been here many times before. I have been here and talked to you many times before. You will know that it must be so, and the very words that you have been listening to now, you have heard many times before. And many times more it will be the same. Souls were never different, the bodies have been constantly dissolving and recurring. Secondly, these things periodically occur. Suppose here are three or four dice, and when we throw them, one comes up five, another four, another three, and another two. If you keep on throwing, there must come times when those very same numbers will recur. Go on throwing, and no matter how long may be the interval, those numbers must come again. It cannot be asserted in how many throws they will come again; this is the law of chance. So with souls and their associations. However distant may be the periods, the same combinations and dissolutions will happen again and again.’4
In the above example, Swamiji, in addition to saying that the die combination {5,4,3,2} is sure to occur somewhere down the line, goes on to comment on the number of throws that one might possibly require to have the same combination once more. This observation quoted above is worth being relooked at: It cannot be asserted in how many throws they will come again; this is the law of chance. We can venture to suggest that these printed words as they appear in the Vol-II of the Complete Works might be a shade insufficient representation of what the Probabilist-sannyasi conveyed. We’ll try to reason it out based on logic and evidence, make an educated guess and leave it at that.
It’s truly amazing how Swamiji
made use of this nascent science
of chance to make some hither-to
unheard-of remarks on
‘Immortality’ of bodies and
forms, hastening to point out
however that ‘that is not the
immortality of the soul.’
For one thing, the sentences ‘It cannot be asserted in how many throws they will come again’ and ‘this is the law of chance’ are somewhat oxymoronic with respect to one another. If a ‘law’ is operative, then it’s ipso facto true that the number of throws can be asserted. To say the reverse is to go back on logic. Granting that it’s the ‘law of chance’, not a deterministic law – even then an emphatic ‘cannot be asserted’ runs counter to the notion of ‘predictiveness’ implicit in the word ‘law’.
More importantly, we’ve reason to believe that Swamiji’s ‘spoken’ words (presumably taken down almost verbatim by Mr. J.J.Goodwin) bearing on this theme are quite different and are indeed closer in spirit to the specific aspect of Probability theory that he was espousing. Here goes a portion of Mr. Goodwin’s transcript of the same lecture ‘The Atman: Its Bondage and Freedom’ which varies in places from the same passage in the Complete Works:
‘Suppose there are three or four dice, and when we throw them one comes up five, and another four, and another three, and another two, and you keep on throwing and throwing. There must come times when those very same numbers will recur. Go on throwing, and no matter how long may be the interval, those numbers must come again. It can be mathematically asserted in how many throws they will come again; this is the law of chance.’5
If, in the italicised sentence above, we care to read ‘mathematically’ as ‘probabilistically’ (with Probability theory yet to be recognized as an independent discipline distinct from Mathematics, Swamiji must have been using these two words almost interchangeably as a matter of loose convention), it would clearly convey the sense in which Swamiji meant ‘the number of throws’ required to have the repetition of the outcome {5,4,3,2}. To all intents and purposes, Swamiji implied the ‘expected value’ of throws – rather than the exact value. Now, in a random process (a process in which ‘law of chance’ is operative) it is not possible to come up with the exact number of throws – it is however possible to find an ‘average’ number of such throws based on the law of probability. In probability parlance, this is known as the ‘expected value’. Let us try to wrap our minds around what Swamiji was hinting at:
Here we’ve the situation of throwing four dice simultaneously. The outcome of the first throw happens to be {5,4,3,2}. In the subsequent throws, let us designate this outcome as a ‘success’ and any other outcome as ‘failure’. Let’s further assume the probability of success is p. The probability of failure is therefore (1-p). Given this set-up, we are interested in knowing the throw-number at which the next success occurs. Now, defining the variable (rather, random variable as the underlying experiment is random) X as the throw-number at which the next success occurs, the required probability that the next success happens at X=x , conditioned on the fact the first success occurred at the first throw is :
P (X=x|The first throw is a success) = p(1-p)x-2 ; x=2,3,……∞
It’s easy to verify that the above is a probability mass function as
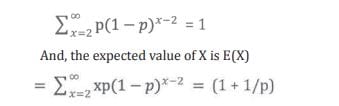
Now, it’s this expected value (1+1/p) that would act as a fair representation of the throw number at which the second success occurs. If we consider each die to be fair, then p = 1/64 . In that case, the average value of the throw number at which the second success takes place is (1 + 64 ) = 1297. In conclusion, our educated guess is that Swamiji meant this expected value of throws when he said ‘it can be mathematically asserted in how many throws they will come again; this is the law of chance.’
The foregoing discussion is surely indicative of the effortless ease with which Swamiji handled some of the important concepts in Probability theory. Against the backdrop that this rather abstruse theory was confined to the rarefied academic circles during nineteenth century, it is all the more extraordinary that a sannyasi could master this almost to the point of expertise. This expertise was such as to have brought out unstinted compliment from no less a Logician-cumProbabilist as Dr. John Venn of University of Cambridge, England. While not much is known about Swamji meeting any great Mathematician or Probabilist in the West, we know for a fact that in England Swamiji met Dr. John Venn – the celebrated authority on Logic and the author of ‘Logic of Chance’. The ‘Venn diagrams’ – inseparable part of Probability theory are named after this great logician. According to the account of Mahendranath Datta (Swamiji’s younger brother): ‘Swamiji impressed the professor very much and he was most pleased with the encounter.’6 Given this mutual admiration, one would not be far out in saying that it was the meeting of a Probabilist from the East with a Probabilist from the West!
Epilogue
As we reflect on Swamiji’s exceptional ability to master even a secular science such as Probability-theory, we simply are mystified as to the source of such power. Sister Christine makes an exegetical comment on this extraordinariness of Swamiji: ‘Others may be brilliant; his mind is luminous, for he had the power to put himself into the immediate contact with the source of all knowledge. He is no longer limited to the slow process to which ordinary human beings are confined.’7
That settles it then! Living as he did in the resplendent glory of the Self, Swamiji’s ‘luminous’ mind was ever in touch with the fount of knowledge and he was thus able to master anything and everything with unstudied grace. His life is indeed a great object lesson that establishes that the Atmajnani (knower of the Self) can easily attain to any knowledge, if he so wishes. Small wonder, his exhortation in this regard (as always) comes laden with his own experiential certitude: ‘Try to manifest this Atman, and you will see your intellect penetrating into all subjects. The intellect of one who has not realised the Atman is onesided, whereas the genius of the knower of Atman is all-embracing. With the manifestation of the Atman you will find that science, philosophy, and everything will be easily mastered.’8
Let us put forth our best energies in manifesting this Atman in every walk of life – academic or otherwise. Then alone can we count ourselves as worthy followers of this master Probabilist-sannyasi for whom the only ‘certainty ’, amidst the probabilistic uncertainties of phenomenal existence, is ‘Atman’ which he never tired of pointing out: ‘The soul endureth forever.’9
References
1) Reminiscences of Swami Vivekananda by His Eastern and Western Admirers [hereafter Reminiscences]. Kolkata: Advaita Ashrama,Mayavati, Fifth Edition, pp.302
2) The Complete Works of Swami Vivekananda [hereafter CW]. Kolkata: Advaita Ashrama, Mayavai Edition, 2: 229-230
3) CW. 2:231
4) CW. 2:260
5) Swami Vivekananda in the West: New Discoveries. Marie Louise Burke. Kolkata: Advaita Ashrama, 3:555-556
6) Londone Swami Vivekananda. [Bengali] Mahendranath Datta, The Mahendra Publishing Committee, pp.43-44
7) Reminiscences. p.329
8) CW. 2:138
9) CW. 4:246
Source : Vedanta Kesari, January, 2020







Leave A Comment